【鉴赏】LongCat-Flash – Samuel 拾光札记

标题: LongCat-Flash Technical Report[1]

LongCat-Flash 共 560B 参数量，激活 18.6B–31.3B 参数量的模型，平均 27B 参数量。比较注重计算效率和 Agent 能力。采用了两种不同的架构设计：zero-computation experts 和 shortcut-connected MoE (scMoE)。训练方法上对模型尺度变换进行了方差修正，并提出了一些训练稳定性技术。

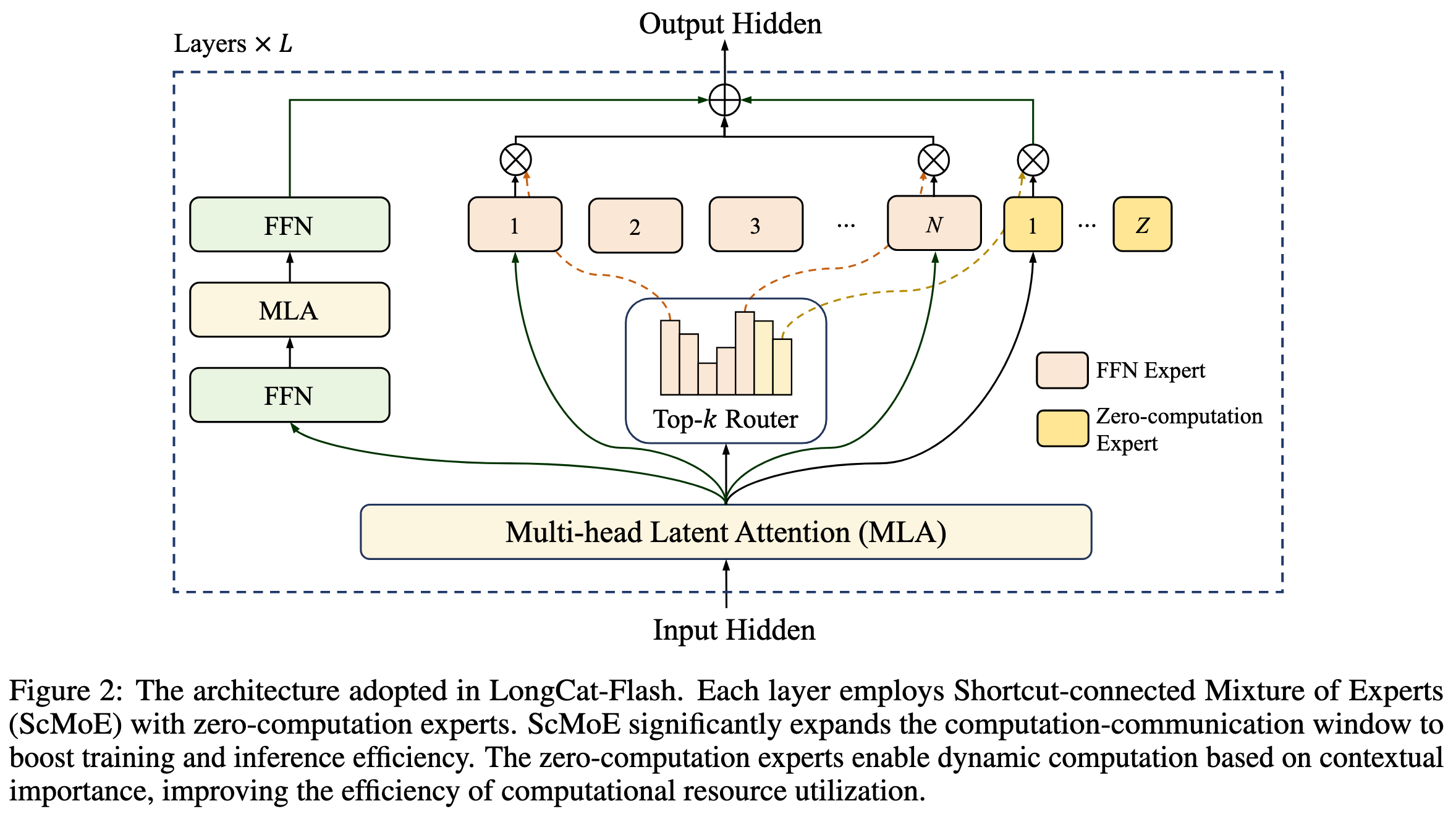
1. Zero-computation Experts

不是每个 token 都是平等的。deepseek v3.2 exp 的稀疏注意力也是这个思想。困难的 token 需要更多的资源进行准确预测。而更容易的 token 则需要忽略一些计算。

$\begin{aligned} \operatorname{MoE}(x_t) &= \sum_{i=1}^{N+Z} g_i \, E_i(x_t), \\ g_i &= \begin{cases} R(x_t)_i, & \text{if } R(x_t)_i \in \operatorname{TopK}\bigl(R(x_t)_i + b_i \bigm| 1 \leq i \leq N+Z, K\bigr), \\ 0, & \text{otherwise}, \end{cases} \\ E_i(x_t) &= \begin{cases} \operatorname{FFN}_i(x_t), & \text{if } 1 \leq i \leq N, \\ x_t, & \text{if } N < i \leq N+Z, \end{cases} \end{aligned} \\$

总的专家数 $K$应该是固定的。只是 $N$ 和 $Z$ 的比例不同。简单的 token，$Z$ 大一点，复杂的 token，$Z$ 就小一点。（感觉这可能会很难训练）

1.1 预算控制

通过专家偏置[2]来进行控制：

$\Delta b_i = \begin{cases} \mu \left( \dfrac{K_e}{K} \cdot \dfrac{1}{N} - \dfrac{T_i}{T_{\text{all}}} \right), & \text{if } 1 \leq i \leq N, \\ 0, & \text{if } N < i \leq N+Z, \end{cases} \\$

其中，$T_{all}$ 表示 $batch$ 数量，$T_i$ 表示被路由到第 $i$ 个专家的数量。$K_e$ 表示 FFN 专家的数量，$K$ 表示总的专家数量。

（相当于路由到这个专家的 tokens 越多，偏置项 $b$ 就越小，后续这个专家的得分就越低。但是这会受到数据混合策略的影响，如果一个 batch 中所有数据都是和 code 相关的，可能就会导致这个偏置项过低，影响后续 code 数据被路由专家。所以说在训练时感觉需要注意数据的混合策略，可以分组混合而不是随机混合。）

偏置项的更新通过 PID （Proportional-Integral-Derivative）控制器来实现。确保第 $i$ 个专家的 token 分配收敛到目标概率。随着专家数量的扩大，这种机制提高了 Softmax 路由概率分布的鲁棒性。但是，零计算专家的偏置项不参与更新，当 FFN 专家收敛后自然就能满足约束。

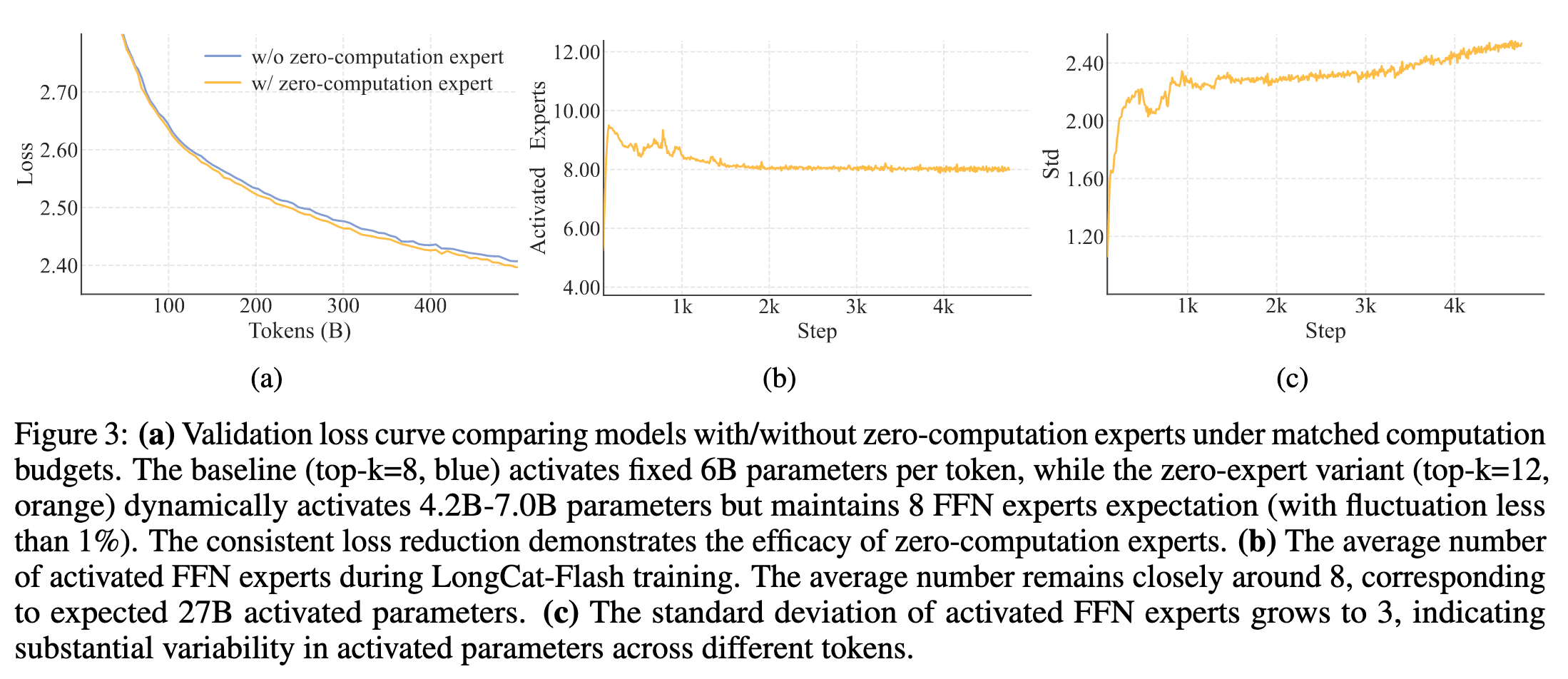
1.2 负载均衡

预算控制中的 $b_i$ 可以实现语料水平的负载均衡。为了进一步防止 EP 组（Expert Partition groups，专家分组）在 “序列级别” 出现极端不均衡，引入了设备级负载均衡损失。

假设所有 $N$ 个 FFN 专家被划分为 $D$ 组，每组包含 $G= \frac{N}{D}$ 个专家。此外，所有零计算专家被归为第 $D+1$ 组。负载均衡损失 $\mathcal{L}_{\text{LB}}$ 由以下部分构成：

$\mathcal{L}_{\text{LB}} = \alpha \sum_{j=1}^{D+1} f_j P_j \\$

$P_j = \frac{1}{T} \sum_{i \in \text{Group}_j} \sum_{t=1}^{T} R(x_t)_i \\$

$f_j = \begin{cases} \frac{D}{K_e T} \sum_{t=1}^{T} \mathbb{I}(\text{token } t \text{ selects Group}_j), & \text{if } 1 \leq j \leq D, \\ \frac{1}{(K - K_e)T} \sum_{t=1}^{T} \mathbb{I}(\text{token } t \text{ selects zero-computation experts}), & \text{if } j = D + 1, \end{cases} \\$

2. Shortcut-connected MoE

参考[3]，主要是为了缓解专家并行的通信开销。有三种连接方式：

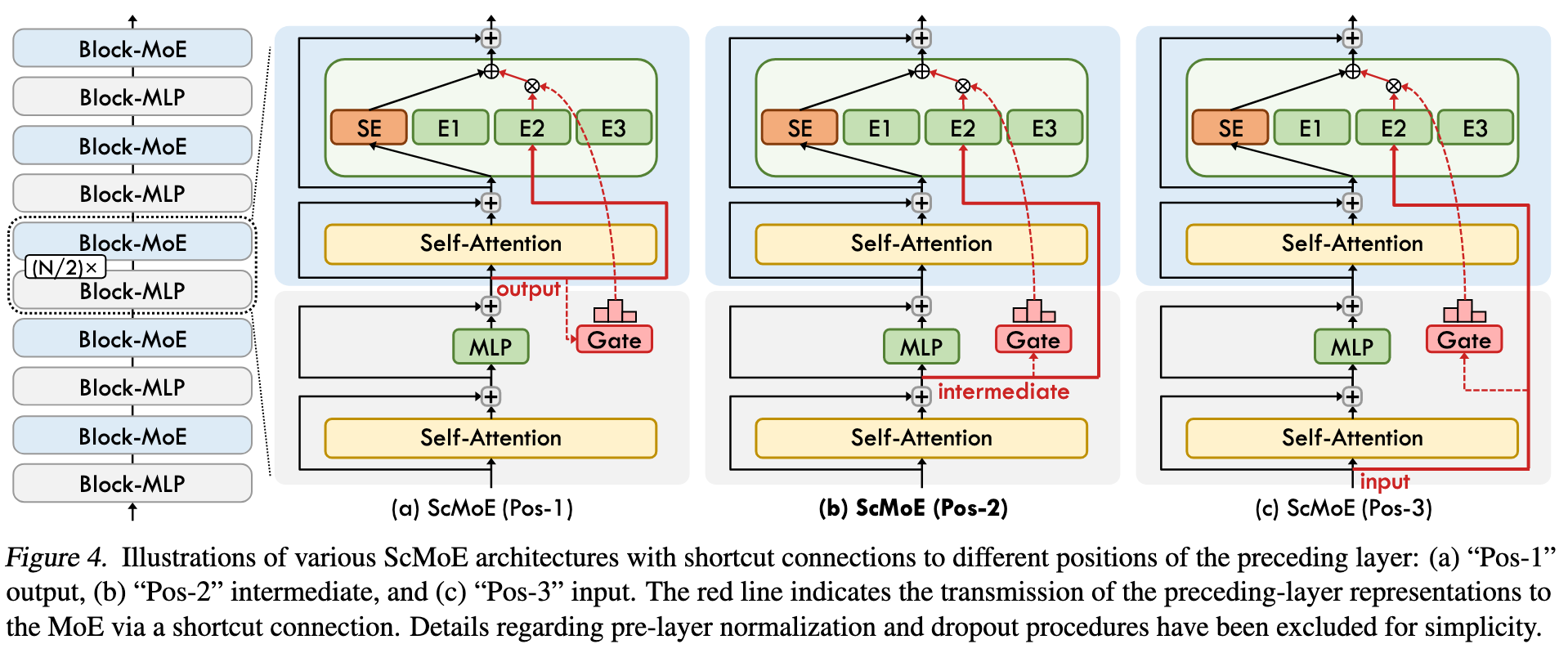
报告里没说是哪一种，不过实验验证了 scMoE 并不会降低模型效果。

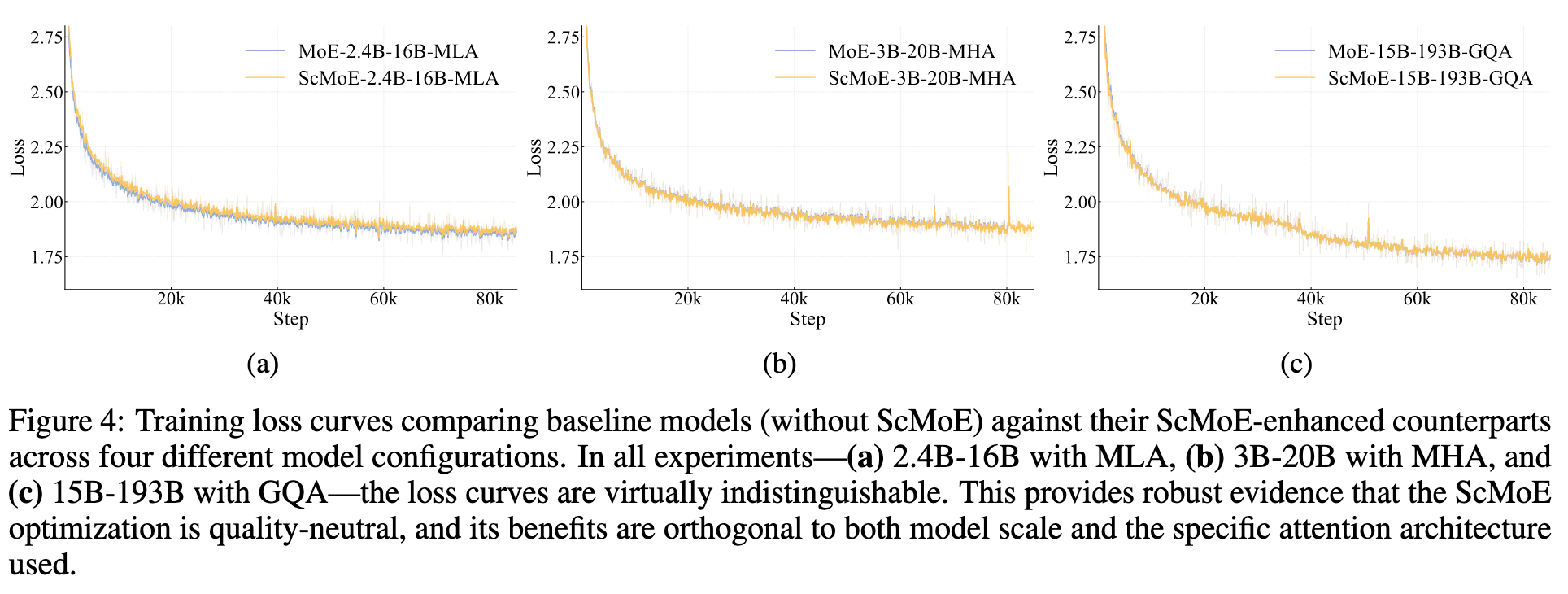
而且，这种架构为推理和训练提供了显著的系统级效率的提升🧐。

3. Variance Alignment Design for Scalability

小尺度模型上的架构设计随着模型尺度的增大可能会变得次优，LongCat 团队经过大量实验和理论分析，验证了特定模块的方差失调是导致这种现象的主要原因。所以，他们提出了 MLA 和 MoE 中的方差对齐技术。

3.1 Scale-Correction for MLA

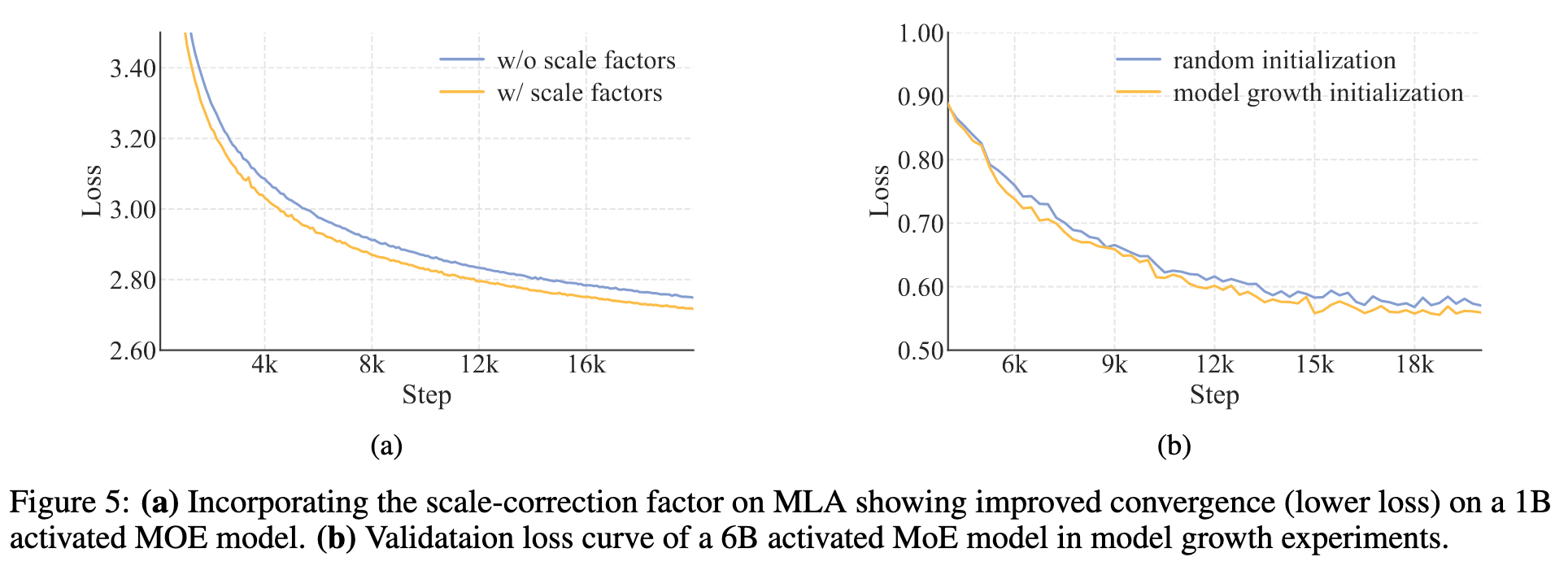
加入尺度矫正因子 $\alpha_q$ 和 $\alpha_{kv}$ 来解决低秩分解中的方差失调问题。

$\begin{aligned} c_t^Q &= \boxed{\alpha_q} W^{DQ} h_t \in \mathbb{R}^{d_q}, & c_t^{KV} &= \boxed{\alpha_{kv}} W^{DKV} h_t \in \mathbb{R}^{d_{kv}}, \\ q_{t,i}^C &= W^{UQ} c_t^Q, & k_{t,i}^C &= W^{UK} c_t^{KV}, & v_{t,i} &= W^{UV} c_t^{KV}, \\ q_{t,i}^R &= \operatorname{RoPE}(W^{QR} c_t^Q), & k_t^R &= \operatorname{RoPE}(W^{KR} h_t), \\ q_{t,i} &= \left[ q_{t,i}^C \, ; \, q_{t,i}^R \right], & k_{t,i} &= \left[ k_{t,i}^C \, ; \, k_t^R \right], \\ o_{t,i} &= \operatorname{Attention}(q_{t,i}, k_{1:t,i}, v_{1:t,i}), & u_t &= W^O \left[ o_{t,1} \, ; \, o_{t,2} \, ; \, \dots \, ; \, o_{t,n_h} \right], \end{aligned} \\$

$\alpha_q = \left( \frac{d_{\text{model}}}{d_q} \right)^{0.5} \quad \text{and} \quad \alpha_{kv} = \left( \frac{d_{\text{model}}}{d_{kv}} \right)^{0.5} \\$

在初始化时，方差与维度成比例：$\sigma^2(q_t^C)$，$\sigma^2(q_t^R) \propto d_q$；$\sigma^2(k_t^C) \propto d_{kv}$，$\sigma^2(k_t^R) \propto d_{\text{model}}$。当 $d_q$、$d_{kv}$ 和 $d_{\text{model}}$ 发生变化时，这种维度差异会在初始化时导致注意力分数不稳定，进而在模型缩放过程中造成性能下降且不可预测。

3.2 Variance Compensation for Experts Initialization

LongCat-Flash 采用类似 DeepSeek-MoE 细粒度专家的策略，但是这种策略对结构的选择比较敏感。所以，他们提出了一种方差补偿机制，以抵消专家分割导致的初始化方差减少。

$\operatorname{MoE}(x_t) = \gamma \left( \sum_{i=1}^{mN} g_i \cdot E_i(x_t) \right) \\$

其中 $g_i$ 是对 $mN$ 个细粒度专家的路由输出，$N$ 表示分割前专家的总数。

$\gamma$ 是通过量化方差减少的两个主要来源来计算的：

门控：将每个原始的 $N$ 个专家分解为 $m$ 个更细粒度的专家，会将专家总数扩展到 $mN$。Softmax 就会在更大的专家池中分配其概率质量，按比例降低单个专家权重 $g_i$ 的大小。因此，输出方差大约降低了 $m$ 倍。
维度：每个细粒度专家的中间隐藏维度（$d_{\text{expert\_inter}}$）降低了 $m$ 倍。假设参数初始化均匀，单个专家的输出方差也会降低 $m$ 倍。

为了在初始化时保持 MoE 层的输出方差，$\gamma$ 必须补偿这两种效应。因此，组合方差补偿因子为 $\gamma = \sqrt{m \cdot m} = m$。

4. 参数初始化

先随机初始化一个小模型，然后再堆叠小模型继续训练。实验验证这种方法比随机初始化效果更好（上面图5）。LongCat 团队认为主要有两个原因：

较小模型的更快收敛可能为大规模训练提供更高质量的参数初始化。
模型规模增大可能引入额外的正则化效果。

5. 训练稳定性

5.1 MoE 路由稳定

给 token 分配更合适的专家（LM）
token 分配到的专家更均匀（LB）

为了平衡上述两种损失，引入了梯度正则比例：

$R_g = \frac{\|\alpha \nabla_{\vec{P}} \mathcal{L}_{\text{LB}}\|_2}{\|\nabla_{\vec{P}} \mathcal{L}_{\text{LM}}\|_2} \\$

其中 $\mathcal{L}_{\text{LB}}$ 是在不考虑系数 $\alpha$ 时计算的负载均衡损失，$\vec{P}$ 是每个 batch 专家概率向量（门控网络的 logits 经过 Softmax 得到）的平均值。

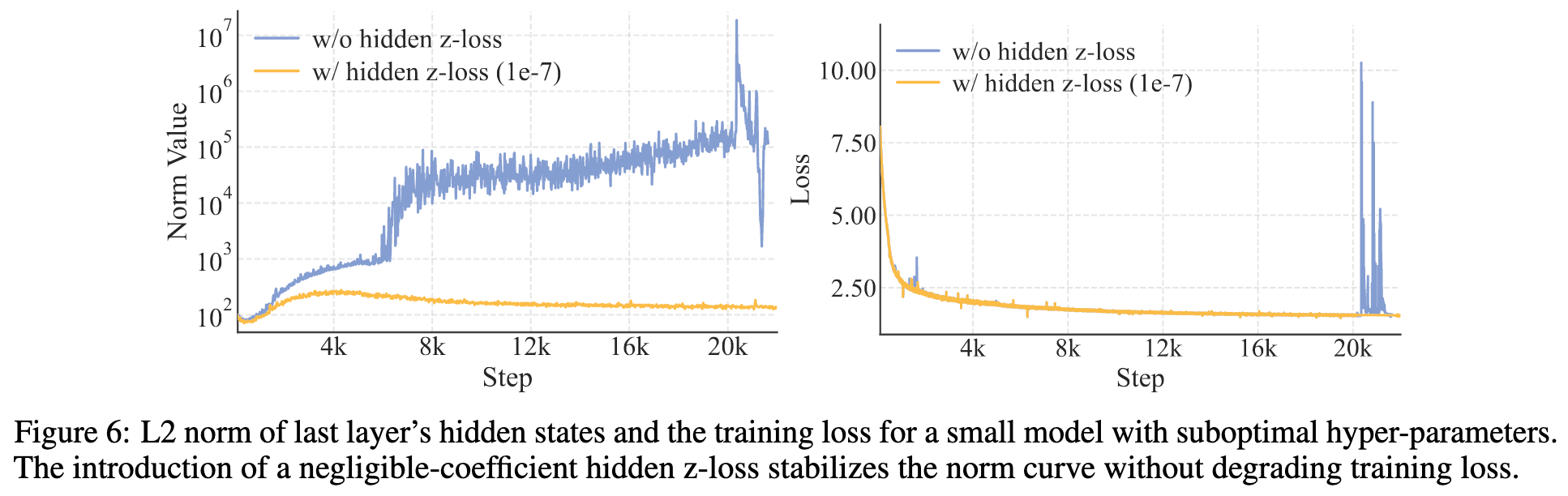
5.2 激活值稳定

LongCat 团队发现，massive activation 与训练过程中的 loss 峰值有关。所以引入了 z-loss 来抑制不合理的极大值。

$\mathcal{L}_\text{Z} = \frac{\lambda}{T} \sum_{t=1}^{T} \left( \log \sum_{i=1}^{|x_t|} \exp(\text{abs}(x_t^i)) \right)^2 \\$

5.3 优化器稳定

随着模型规模的增大，Adam 中的$ \epsilon $超参数变得越来越重要。通过跟踪梯度的 RMS Norm 发现：当$ \epsilon $接近梯度的 RMS Norm 时，模型效果会显著下降；而更低的$ \epsilon $对模型性能影响不大。实验结果如下图。LongCat-Flash 用的是$ \epsilon=1e-16 $。

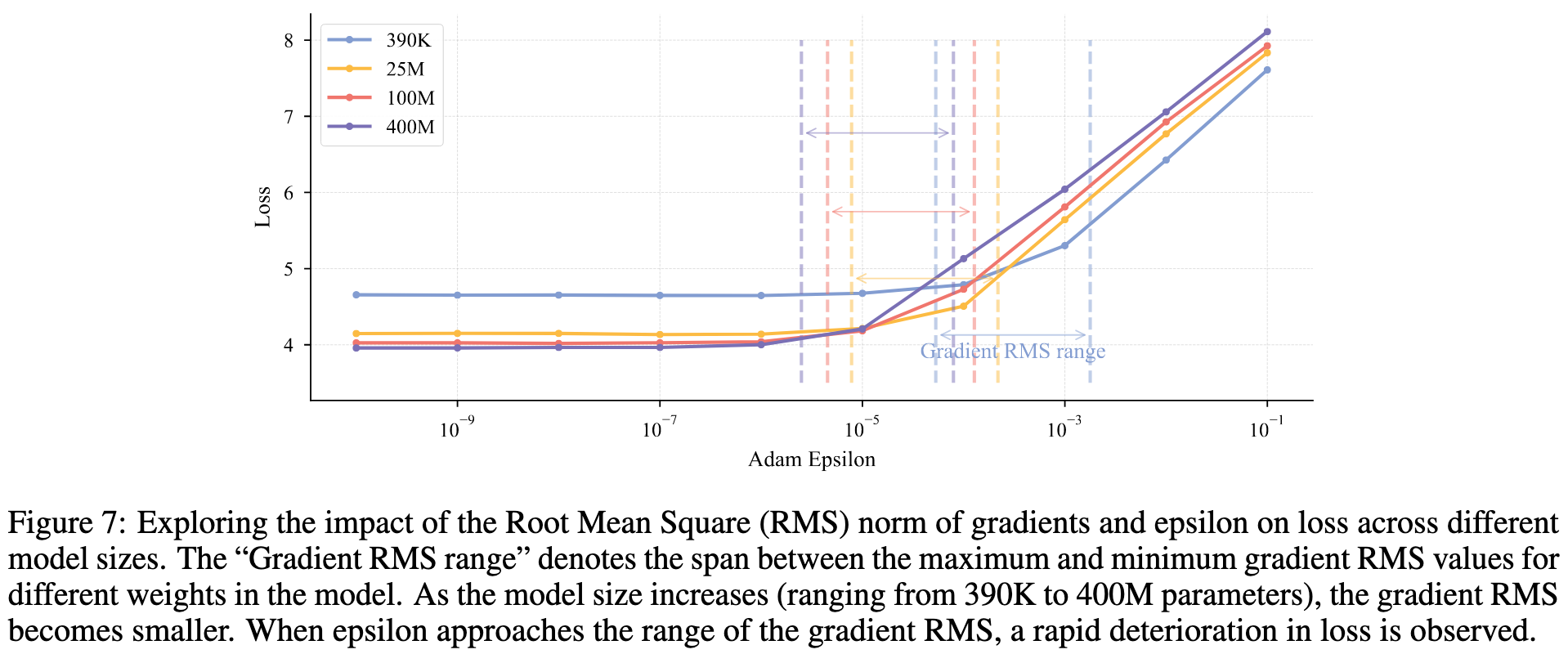
大白话就是，模型规模越大，参数初始化时越小，导致梯度 RMS Norm 越小，所以需要更小的 $ \epsilon $。

6. 笔者总结

技术报告还是挺详细的，从模型架构，训练方法，数据构造等方面都介绍了。模型主要关注推理效率和 Agent 能力，所以整体性能上可能没有那么突出。但是里面用到的一些技术，实验结果，和分析都挺有参考价值的。

归档

分类