标题: DISTILLM-2: A Contrastive Approach Boosts the Distillation of LLMs[1]

FROM ICML 2025 oral arXiv GitHub

在大语言模型的发展进程中，模型蒸馏技术是实现 “高性能与低部署成本” 平衡的关键。DISTILLM-2 横空出世，凭借创新的对比学习损失设计，为 LLM 蒸馏带来全新思路。本文将拆解其核心逻辑，结合公式与实验，带你看透这一前沿方法。

1. 传统蒸馏的痛点：模式崩溃与模式平均

在数据分布里，“模式（mode）” 是概率密度的峰值区域，代表高频出现的特征组合（如 MNIST 中每个数字、人脸数据中不同表情） 。

• 模式平均（Mode Averaging）：正向 KL（ \(KL(p\vert\vert q)\) ）优化时，模型为覆盖真实分布，将多个模式 “平滑平均”，生成样本模糊（如数字既像 “3” 又像 “5” ）

• 模式崩溃（Mode Collapse）：反向 KL（\(KL(q\vert\vert p)\) ）优化时，模型为避免惩罚，仅聚焦少数易学习模式，抛弃数据多样性。比如生成模型只输出 “7”，无视其他数字，让蒸馏后的模型失去泛化性。

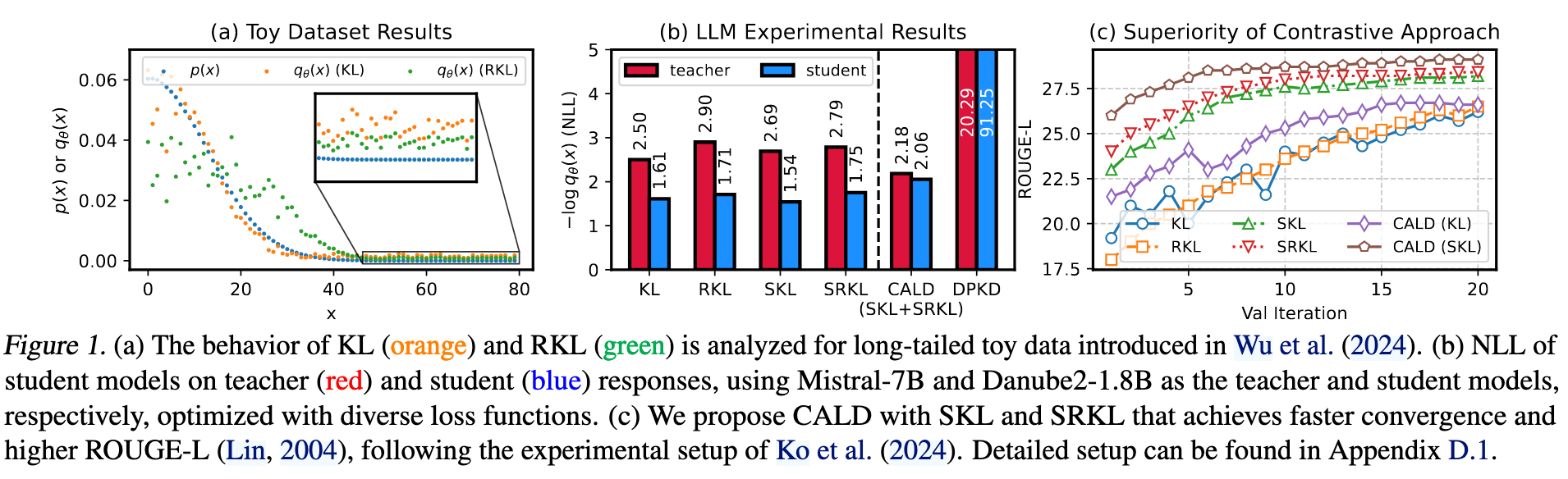
2. DISTILLM-2：对比学习驱动的蒸馏框架

Ko 等[2]提出了 Skew KL (SKL) 和 Skew RKL (SRKL) 进行改进 （感觉就是降低教师模型的比重，学的更平滑一点。但是为什么会加快收敛速度呢？难道是由此避免了不必要的搜索空间？🤔）

\(\mathcal{D}_{\text{SKL}}^{（\alpha）}(x,y;p||q_{\theta}) = \mathcal{D}_{\text{KL}}(x,y;p||\alpha p + (1 – \alpha) q_{\theta})\)

\(\mathcal{D}_{\text{SRKL}}^{（\alpha）}(x,y;p||q_{\theta}) = \mathcal{D}_{\text{KL}}(x,y;q_{\theta}|| (1 – \alpha) p + \alpha q_{\theta})\)

DistiLLM-2 在此基础上进行了改进，损失函数重新定义蒸馏逻辑

\(\mathcal{L}_{\text{DISTILLM-2}} = \frac{1}{2|\mathcal{D}|} \sum_{(\boldsymbol{x}, \boldsymbol{y}_t, \boldsymbol{y}_s) \sim \mathcal{D}} \left[(1 – \beta) D_{\text{SKL}}^{(\alpha_t)}(\boldsymbol{x}, \boldsymbol{y}_t) + \beta D_{\text{SRKL}}^{(\alpha_s)}(\boldsymbol{x}, \boldsymbol{y}_s) \right]\)

将 DPO 的对比学习概念引入 KD。对齐学生模型的输出（SGOs）和教师模型的输出（TGOs）。（就是利用这里的 \(\boldsymbol{y}_t\) 和 \(\boldsymbol{y}_s\) 进行对比学习）

之前就有人这样做过，比如 Li 等[3]提出的 DPKD 在 DPO 中用教师模型替换参考模型，但是频繁遇到 reward hacking。DPKD 论文中并没有提到 reward hacking 问题。

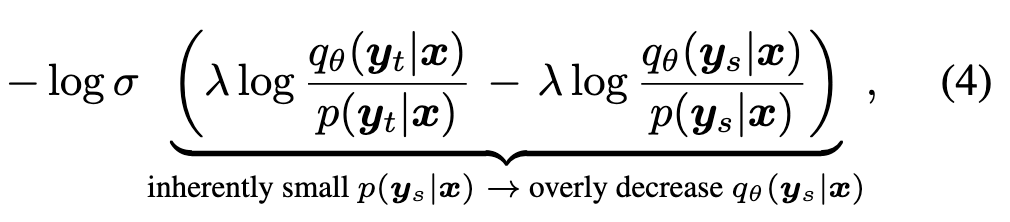
作者的解释是：采用 Equation 4. 这种损失，导致 \(q_\theta(\boldsymbol{y}_s|x)\) 变得很低。学生模型为了拟合教师模型的输出，会丢失原有的知识。（但是这和 reward hacking 有什么关系？🤔）

于是作者提出了 CALD 损失函数。

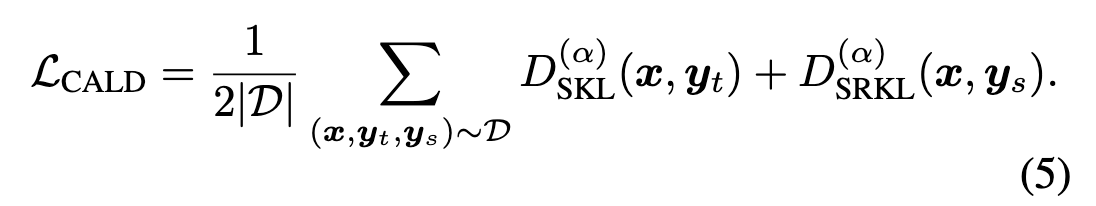
正向 SKL 用教师模型的输出，反向 SKL 用学生模型的输出。简单起见，观察正反向 KL 的公式。

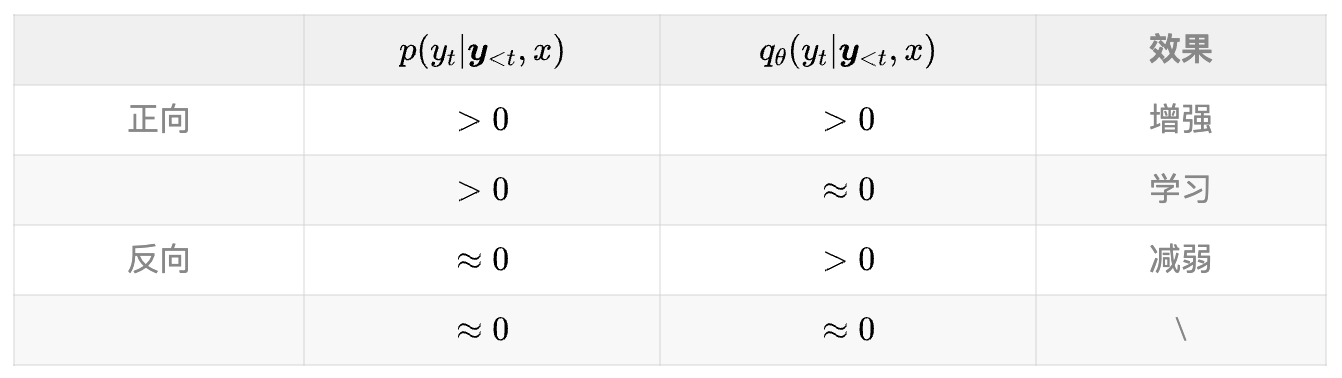
3. 和 DPKD 的对比

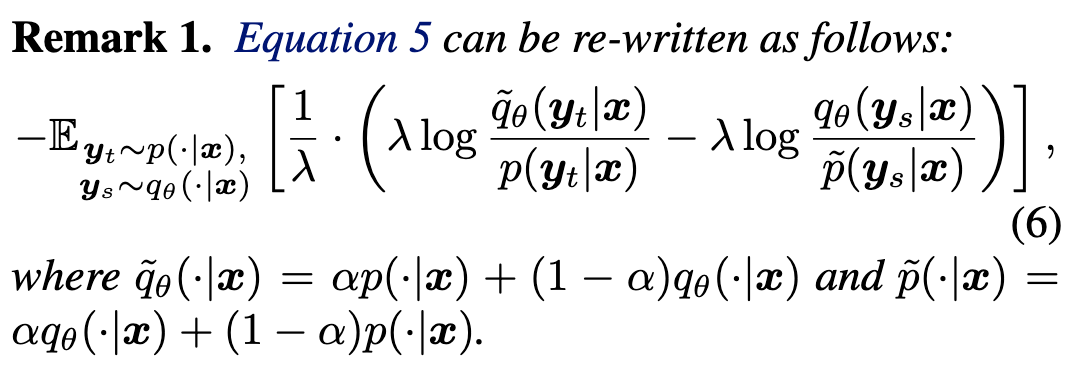
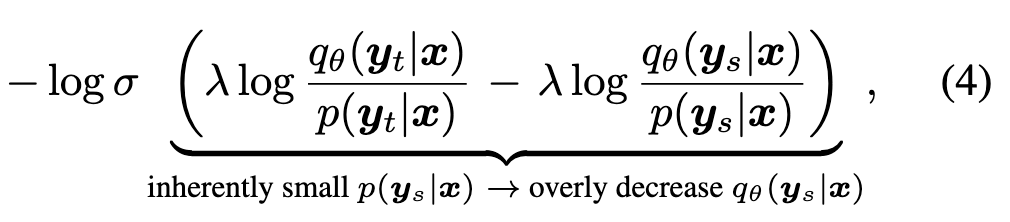
对比 Equation 6. 和 Equation 4.，相当于将 KL 替换为 SKL，然后 log-sigmoid 变成了一个线性变换。\(\tilde{q}_\theta(\cdot \mid \boldsymbol{x})\) 和 \(p(\cdot \mid \boldsymbol{x})\) 之间的线性关系，对过度减小的 \(q_\theta(\boldsymbol{y}_s|x)\) 起到了正则化作用，从而解决了 DPKD 中的难题。 （不是很懂😂，感觉意思是 SKL 平滑过度的性质解决或缓解了 DPKD 导致 \(q_\theta(\boldsymbol{y}_s|x)\) 变得很低的问题）

4. 从 Equation 6. 到 Equation 2.

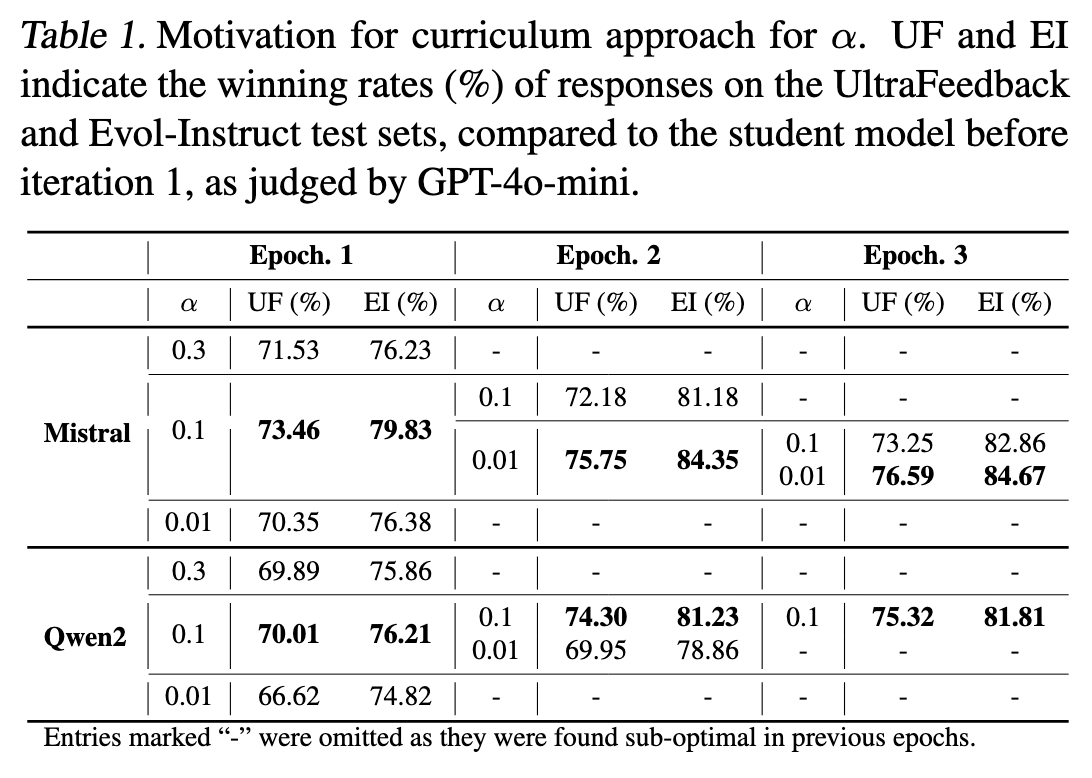
1. \(\alpha\)：较大的 \(\alpha\) 有助于训练的稳定，能加速收敛 （笔者比较疑惑，为什么是一定能加速收敛） 。但是限制了知识的获取 （所以不应该收敛较慢吗） 。作者给了 \(\alpha\) 一个适中的范围 \(0.1-0.3\)。作者对于简单样本（和教师模型分布差异较小）采用较小的 \(\alpha\)，困难样本采用较大 \(\alpha\)（笔者：就是更平滑过渡..） 。作者引入了 Mercator series[4] 来更新 \(\alpha\)。\(\log{p(x)}\) 一阶近似为 \(\log{p(x)}-1\) 。那么就有公式7。

2. \(\beta\)：作者观察到逐渐增加 SRKL 的权重有助于提高学生模型的表现 （先学习后修正，符合直觉） 。于是引入 \(\beta\) 进行调节。观察伪代码，作者是根据 \(epoch\) 和 \(iteration\) 对 \(\beta\) 进行调节的。

5. 实验

在推测生成中，学生模型生成 \(K\) 个 tokens，教师模型根据下面的公式对 tokens 进行验证。

\(q_{\theta}(y_{n + k} \mid \boldsymbol{y}_{< n + k}) > \min(\varepsilon^2, \varepsilon \cdot \exp(-H(p(\cdot \mid \boldsymbol{y}_{< n + k}))))\)

其中，\(H(\cdot)\) 和 \(\varepsilon\) 分别是熵函数和超参数 。

当用 \(\boldsymbol{y}_{spec}\) 替换 \(\boldsymbol{y}_{t}\) 时，只有满足 “学生模型生成该 token 的概率高于 \(\epsilon\) 和 教师模型概率” 时，才接受该 token。\(\epsilon\) 越小，学生模型和教师模型的分布就越相同。

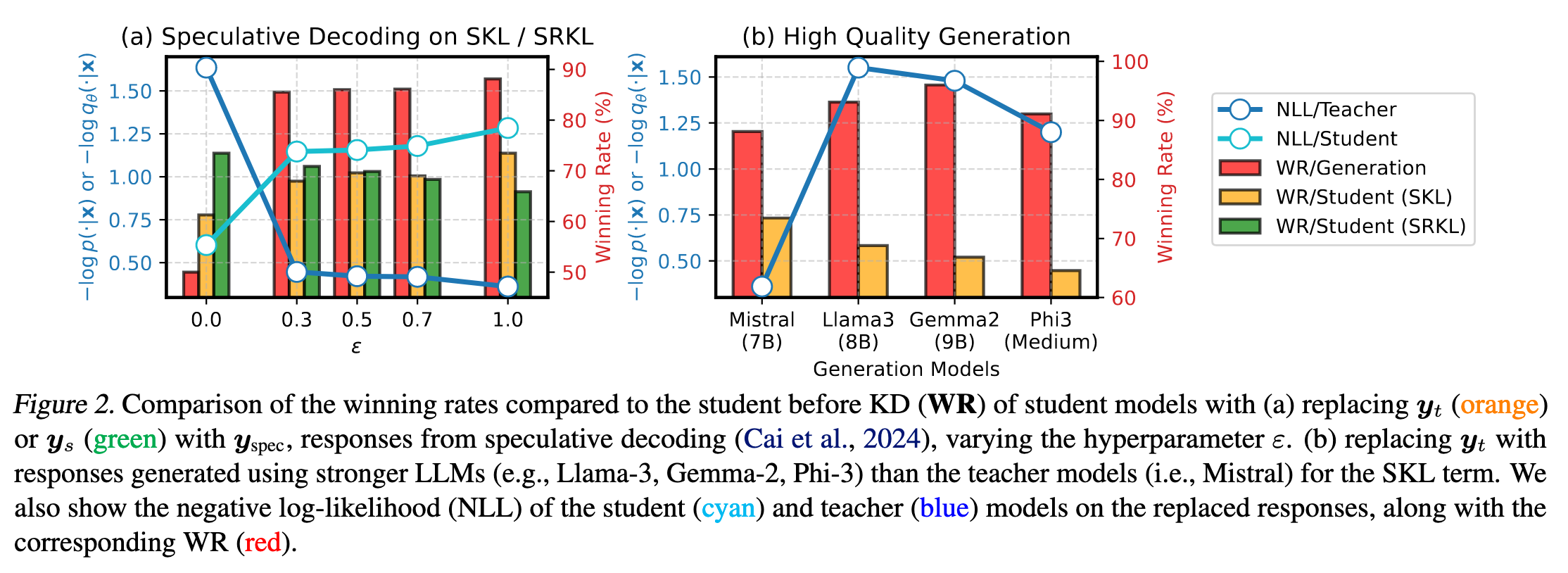
如 Figure 2.，SKL 的下降并不总能带来性能的提升，相反，教师模型 response 的强指导与蒸馏性能高度相关。（笔者猜测有可能是因为教师模型并不是最优模型，学生模型拟合了教师模型较差的知识，导致 SKL 下降而性能下降或不变）

作者还对比了其他的教师模型，如 Figure 2. 所示。教师模型 response 的高对数概率或许是比其更高质量更重要。即使某一 response 质量不错，但如果教师模型生成它时的概率较低（置信度低），其在数据筛选中的价值可能不如那些教师模型高置信度生成的响应 —— 后者更能有效指导学生模型学习。

6. 实验结果

6.1 指令遵循

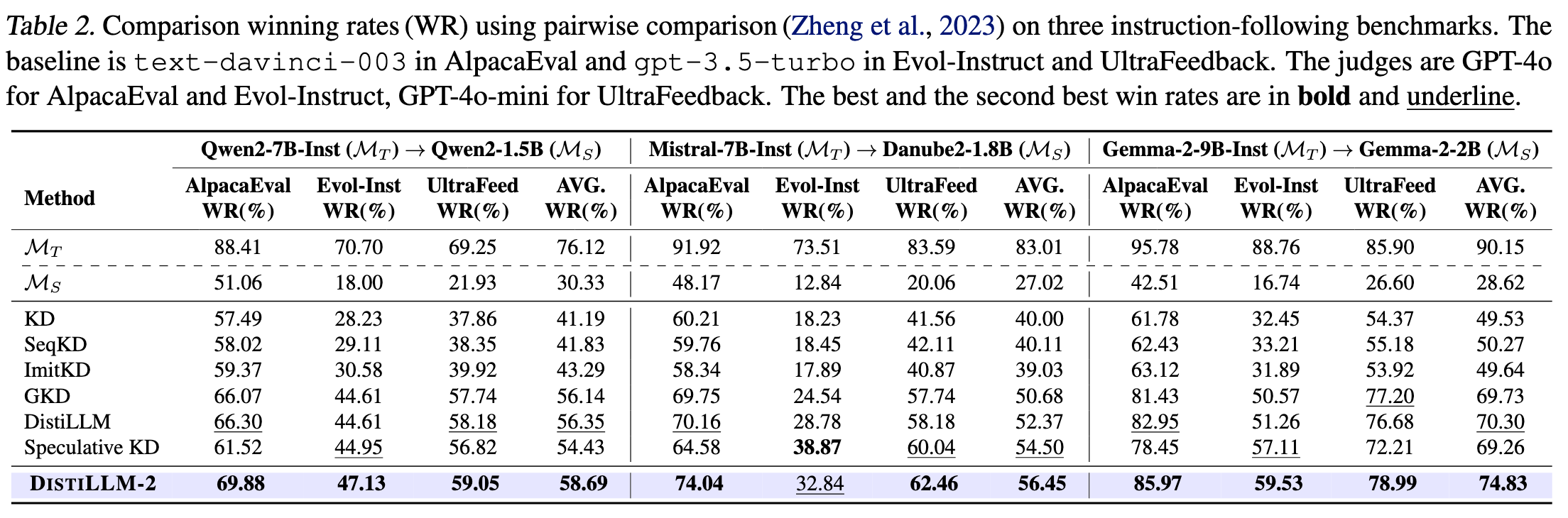
6.2 数学推理

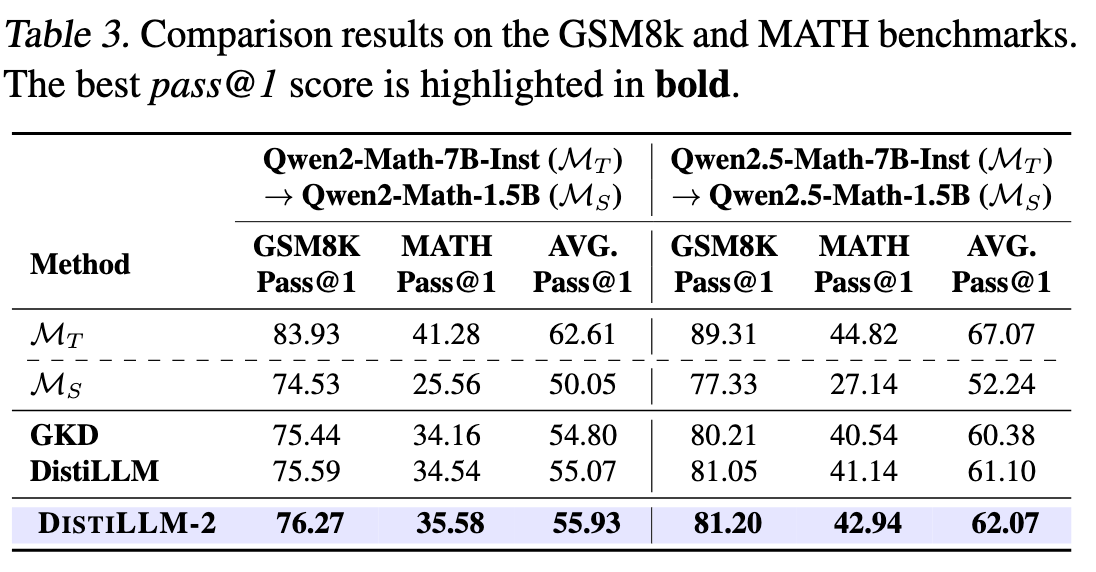
6.3 代码生成

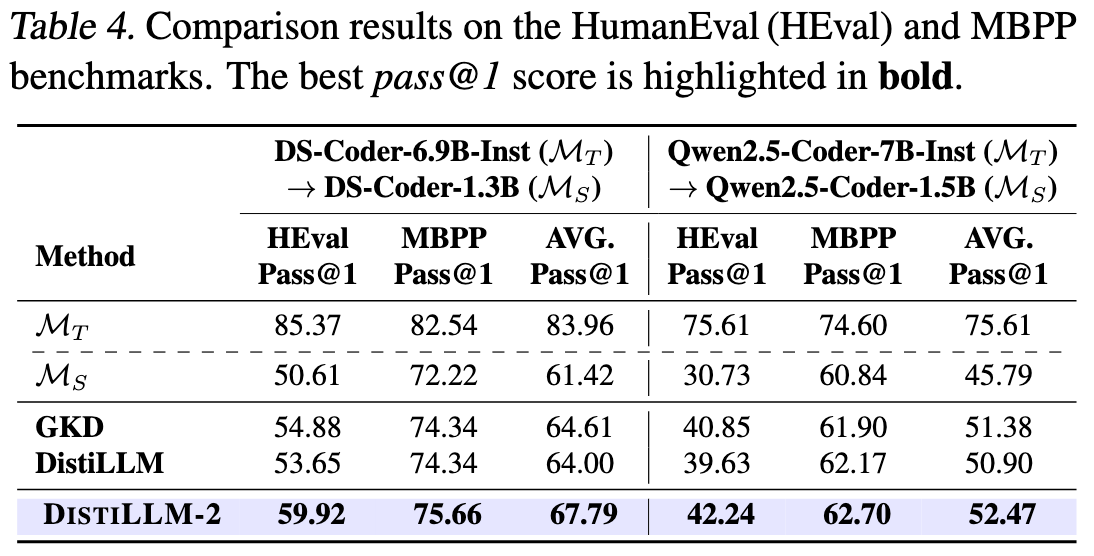
6.4 消融实验-方法

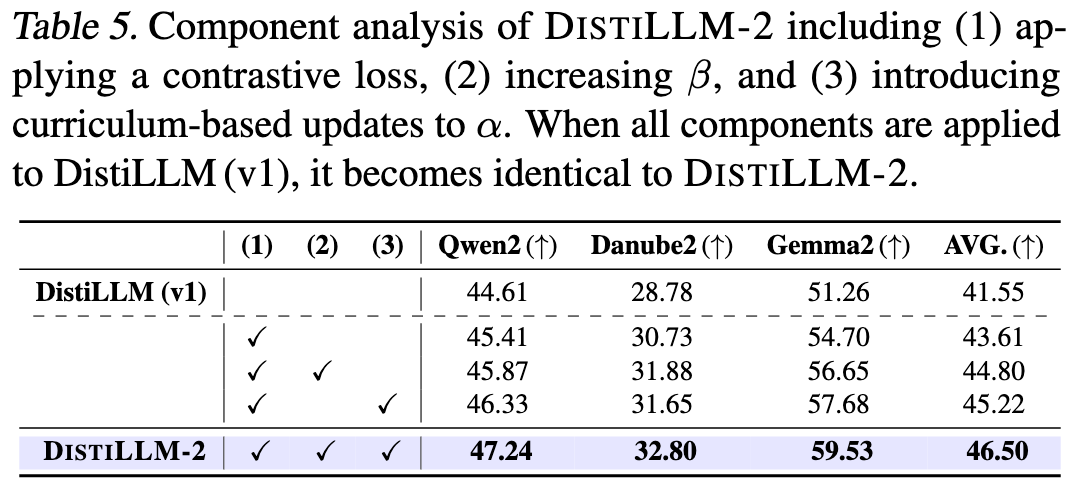
6.5 消融实验-数据

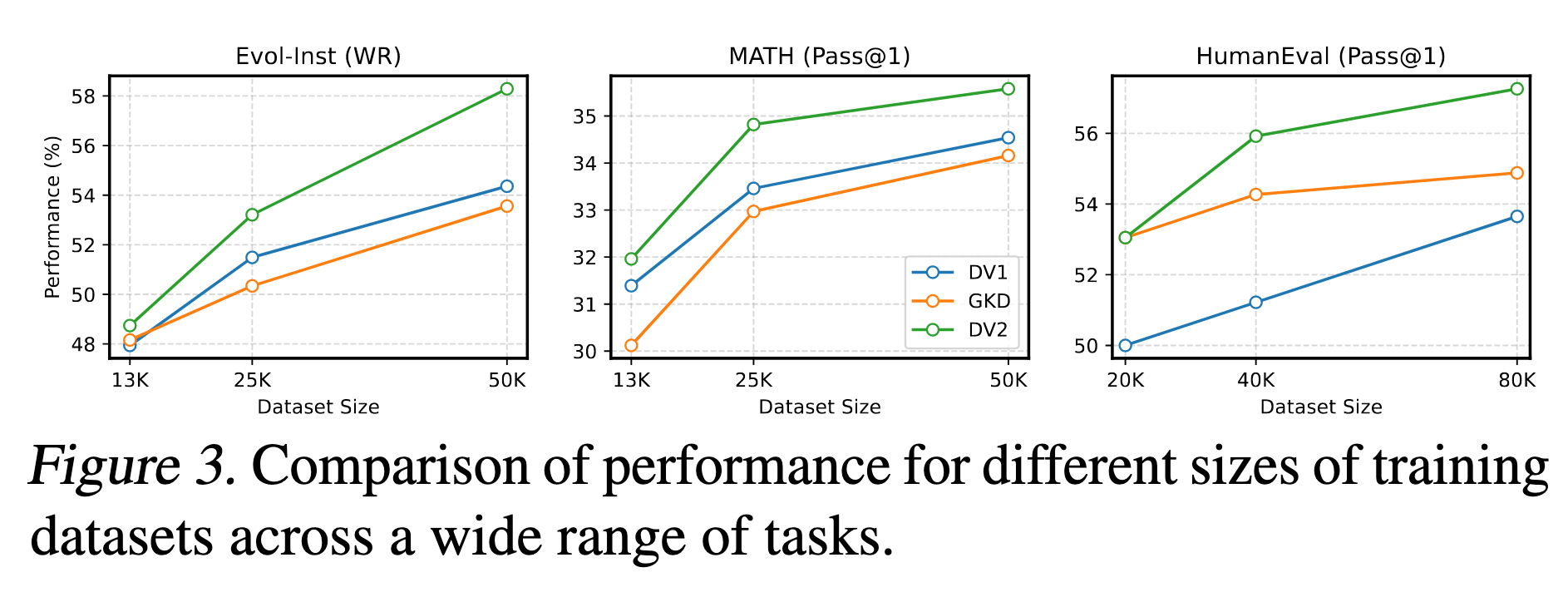
6.6 消融实验-模型

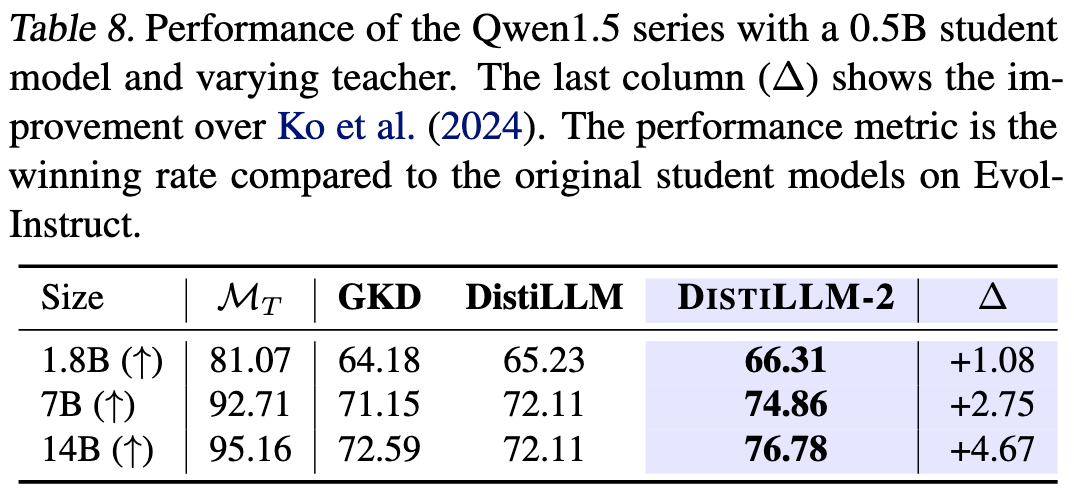
6.7 SFT + DPO 替换为 DistilLLM-2 + DPO

结合 Table 2去看，好像即使是 naive KD 也比 SFT + DPO 效果要好？Why?

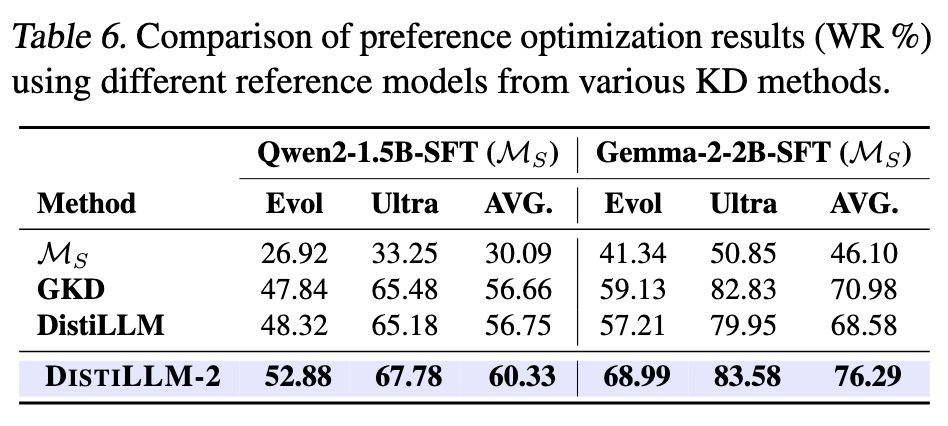
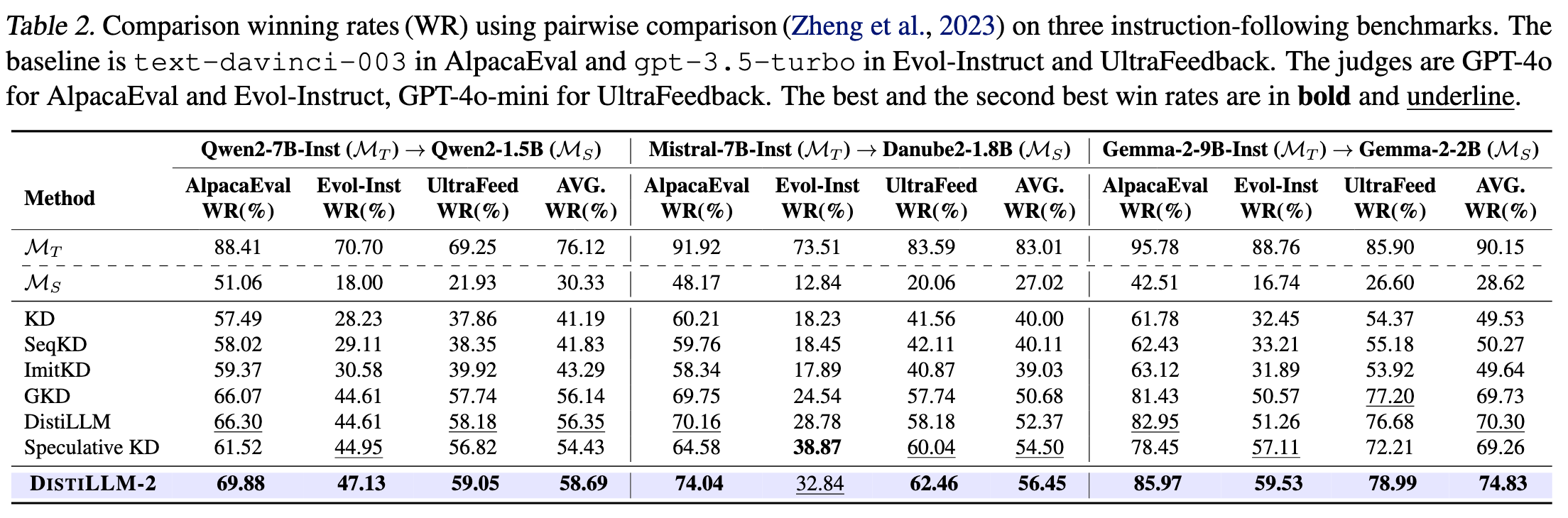
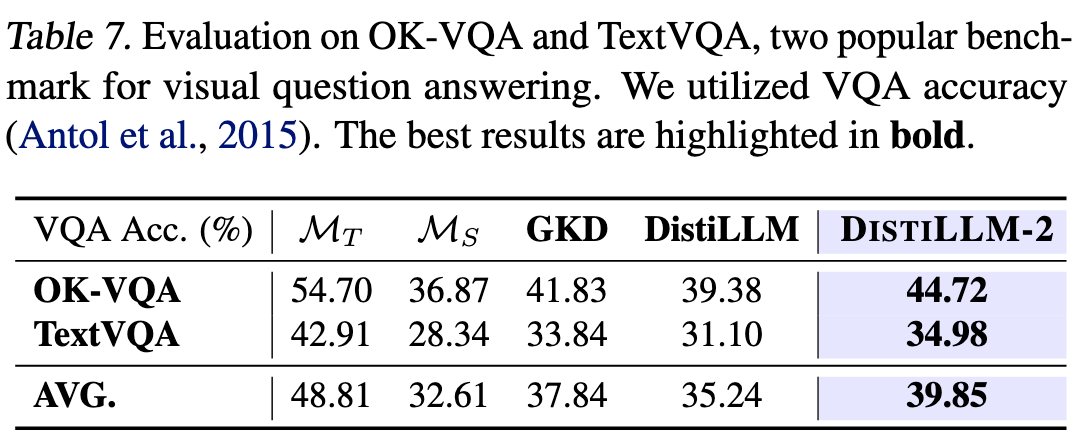
6.8 应用到多模态模型

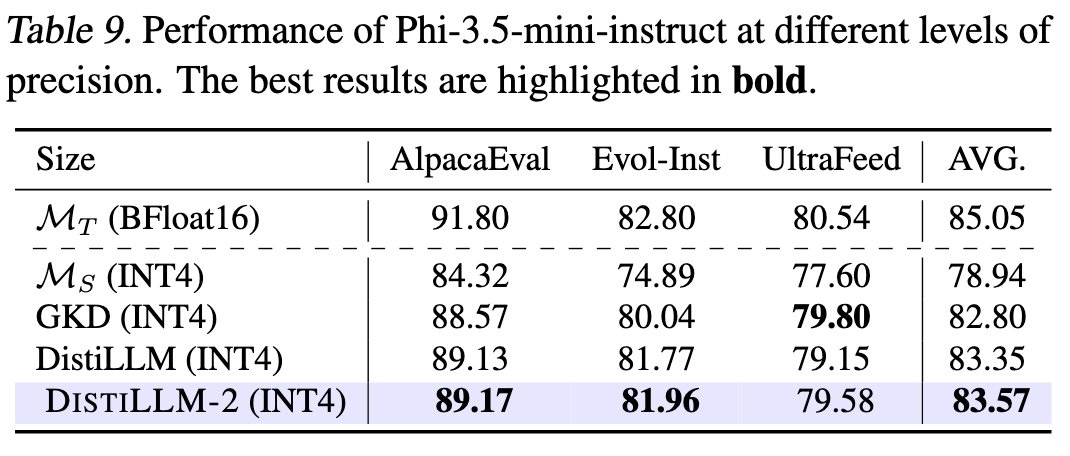
6.9 INT4 量化后用 KD 代替 SFT 恢复模型表现

笔者感觉提高更准确一点。这里应该是 post-training 量化后，再用 FP16 的教师模型进行微调，减小量化误差

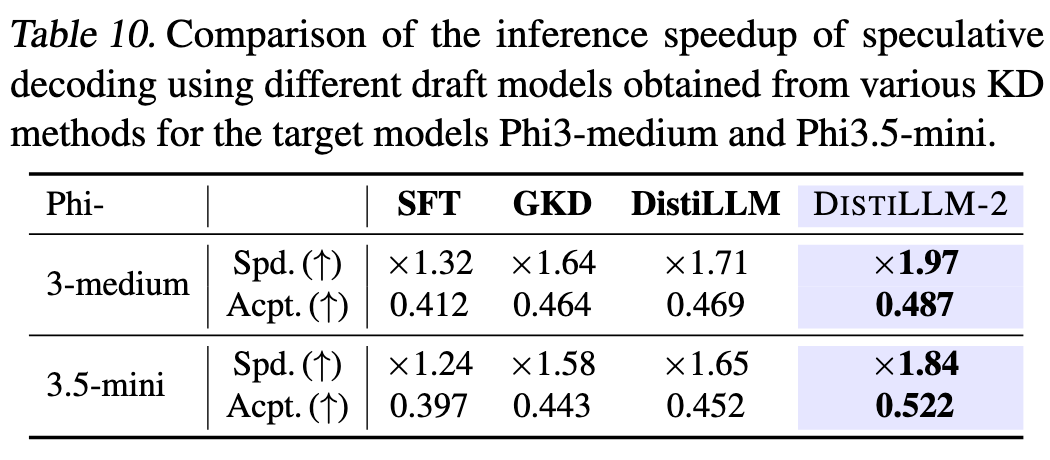
6.10 推理速度

为啥推理速度会变？KD不是只改变学生模型参数吗，和推理速度有什么关系？

7. 笔者总结

1. DistiLLM-2 结合了 SKL 和 SRKL。引入 \(\alpha\) 和 \(\beta\) 优化训练过程。大大缓解了模型平均和模型崩溃，而且提高了模型效果👍。
2. 作者做了大量的对比实验，全方位验证了方法的效果（角度太多了，以后做试验可以参考😂）。
3. 笔者还是有很多没太看明白的地方，比如和 DPKD 对比时为什么是正则作用。看来还是需要勤加修练。

Reviewer: here

References

1. DISTILLM-2: A Contrastive Approach Boosts the Distillation of LLMs
2. DistiLLM: Towards Streamlined Distillation for Large Language Models
3. Direct Preference Knowledge Distillation for Large Language Models
4. CRC Standard Mathematical Tables and Formulae

注：若本文中存在错误或不妥之处，欢迎批评指正。